Математические методы в биологии и медицине

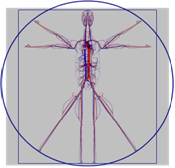
Начало физиологии кровотока связывают с именем английского врача и ученого W. Harvey, который в 1628 году в книге "Exercitatio anatomica de motu cordis et sangninis in animalins" опубликовал свои взгляды на систему кровообращения. В этой книге было представлено для того времени точное и законченное учение, опирающееся на простые и наглядные опыты, о круговороте крови. Последующие исследования сердечно-сосудистой системы велись в нескольких основных направлениях. Одно из них связано с изучением структуры, функций, реактивности одиночных сосудов и выделенных участков кровеносной системы с целью выяснения специфических особенностей, свойственных именно этим частям. Значительное внимание уделялось также исследованиям общих и специфических закономерностей как суммарного кровотока по всей сосудистой системе, так и регионарного кровотока в отдельных частях сердечнососудистой системы, роли и значения выделенных свойств на функционирование кровеносной системы в целом. К настоящему времени накоплен большой объем данных о строении и функциях сосудистой системы, различных видах регуляции кровообращения, сформулированы основные принципы организации системы управления кровообращением. Но многие закономерности деятельности сердечнососудистой системы всё ещё нуждаются в дальнейших исследованиях.

Очевидно, что только качественная интерпретация функций сердечнососудистой системы недостаточна для гарантированного понимания и вмешательства в ее деятельность. Необходимо еще и математическое моделирование заболеваний сердечнососудистой системы, которое позволяет получать количественные зависимости степени проявления симптоматики конкретного заболевания от степени поражения сосудистой системы.

Математическое моделирование кровообращения человека представляет собой сложную и актуальную проблему современной медицины и математики, имеющую высокую как фундаментальную, так и прикладную значимость.

Задача построения общей математической модели сердечнососудистой системы и компьютерных методов ее исследования на данный момент не решена. Прежде всего, это связано с чрезвычайной сложностью рассматриваемой биологической системы, функционирование которой зависит от огромного количества факторов, практически от каждого элемента живого организма, и эти зависимости во многом остаются не формализованными даже на физиологически описательном уровне.

Надо отметить, что все существующие работы в области гемодинамики, помимо построения и разработки собственно моделей, требуют определенных усилий по созданию численных методов решения соответствующих задач, а также связаны с проблемой реализации разработанных методик на ЭВМ. Особое место занимает подготовка вычислительного эксперимента и обработка его результатов.

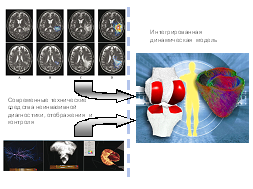
Ключевой проблемой математического моделирования гемодинамических задач является получение достоверных числовых значений физиологических параметров элементов сердечнососудистой системы, что представляет собой отдельную и достаточно сложную и трудоемкую работу.

Увеличение производительности вычислительной техники сделало возможными попытки численного исследования гидродинамики крови в сосуде в трехмерной геометрии, близкой к реальной.

Существует много практически важных медицинских и физиологических проблем, требующих аккуратных и точных расчетов многомерных течений в сосуде. Достаточно упомянуть исследование течения крови в стенозированных и тромбированных сосудах, моделирование кровотока при наличии стентов, шунтов и фильтров, течений в бифуркациях сосудов и при аневризмах.

Большое место в математических моделях гемодинамики занимает математическое описание работы сердца, как важнейшего элемента сердечнососудистой системы. В этой области построено и используется большое количество моделей – от имитационных и простейших одномерных (представляющих сердце как обычный поршень) до трехмерных. Проблема построения таких полноразмерных моделей состоит как в трудности расчета трехмерных гидродинамических процессов в сложной, изменяющейся области (соответствующей желудочкам или предсердиям сердца), так и в необходимости учитывать и воспроизводить свойства мышц сердца, особенности их строения, функции, системы регуляции. Отметим, что объем вычислительной работы в таких моделях весьма велик и возникает необходимость использования высокопроизводительных вычислительных систем.

Существует ряд физиологических и медицинских проблем, исследование которых требует рассмотрения сердечнососудистой системы в целом – методы регуляции артериального давления, гипертензия, кровоснабжение органов (в первую очередь – тканей головного мозга) и многие другие. Особенностью такого моделирования является необходимость учета многочисленных физиологических факторов, влияющих на течение крови, их математической интерпретации, и, как следствие, развитие иерархической последовательности систем моделей. Отдельной проблемой является выбор математического аппарата для построения моделей и адекватных методов их численного решения.

Для описания работы замкнутой сердечнососудистой системы в целом в настоящий момент наиболее привлекательными являются квазиодномерные модели течения крови в сосудах.

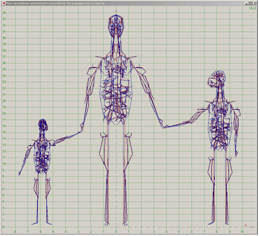
Применение квазиодномерного приближения позволяет рассматривать и численно решать гемодинамические задачи на достаточно разветвленной сети сосудов системы кровообращения (графе сосудов), как незамкнутой, так и замкнутой.

Описание системы сосудов на базе квазиодномерных моделей позволяет, в случае необходимости, совмещать его с двух и трехмерными моделями. Это особенно существенно, если требуется детально исследовать локальную гемодинамическую пространственную картину течения (например, в выделенном сосуде) «встроенную» в интегральную структуру кровообращения.

Современный подход к решению гемодинамических задач кровообращения в целом с учетом дополнительных процессов реализуется в работах на кафедре вычислительных методов. В этих работах предложена постановка задачи моделирования течения крови по разветвленной системе сосудов, представляющей оба круга кровообращения, предложен и реализован численный алгоритм решения квазиодномерных уравнений гемодинамики в совокупности с расчетом транспорта кислорода по системе кровообращения на графе сосудов. Правильное воспроизведение скорости кровотока по сосудистой сети предоставляет возможность моделировать распространение различных веществ в полной сердечнососудистой системе или ее разветвленной части и влияние этих веществ на гемодинамику в целом, воспроизводить в вычислительном эксперименте перераспределение содержания кислорода в крови, ферментов, лекарственных препаратов.

Квазиодномерная модель, описывающая движения крови в сосуде, обычно включает в себя три уравнения. Два уравнения выражают законы сохранения (закон сохранения массы крови и закон сохранения количества движения). Эти уравнения не зависят от физиологических свойств сосуда и справедливы для сосудов с любыми характеристиками. В качестве третьего уравнения обычно используют соотношение, связывающее площадь поперечного сечения сосуда и трансмуральное давление (разница давлений внутри и снаружи сосуда) в сосуде. Именно в этом уравнении, которое называют уравнением состояния, учитываются все присущие данному типу сосуда свойства.

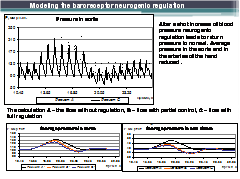
Целью работ является создание на базе современных информационных технологий компьютерной физиологически адекватной модели сердечнососудистой системы человека для последующего использования ее, например, при создании тренажерно-диагностических комплексов, используемых для обучения студентов медицинских специальностей, профилактических обследований состояния сердечнососудистой системы, диагностики и как пред-, так и интро-операционной оценки параметров течения крови в сердечнососудистой системе в целом или в отдельных ее разделах.

При выполнении этих работ помимо создания математических моделей и эффективных вычислительных методов необходимо было организовывать обработку потока входной и выходной информации как в числовом, так и в графическом виде и разработать интерфейсную среду с интерактивным режимом общения с пользователем.

Работа по созданию симулятора кровообращения реального человека привела к пониманию того, что для достижения этой цели необходимо реализовать следующие возможности:

1) Представление произвольного трехмерного графа сердечнососудистой
системы, в том числе в целом, с возможностью его наращивания,
а также сужения;

2) Перемещение графа в целом, а также его частей в пространстве для учета
влияния гравитации при изменении положения тела;

3) Использование реалистичных объемных 3D моделей для визуализации
системы сосудов и результатов расчета в привычной наглядной форме;

4) И, как следствие, разработка развитых средств редактирования, хранения
и контроля существенно возросшего объема вводимых данных;

5) Многопоточная (multithread) реализация комплекса для распараллеливания
процесса вычислений и визуализации его результатов.

Руководители

Буничева Анна Яковлевна

Мухин Сергей Иванович

Соснин Николай Васильевич

Хруленко Александр Борисович