Семинар

«Современные прикладные задачи механики сплошной среды»

Научные руководители:

д.ф.м.н., доцент кафедры вычислительных методов

Абакумов Михаил Владимирович,

д.ф.м.н, г.н.с. ИПМ им. М.В.Келдыша, профессор кафедры вычислительных методов

Мажорова Ольга Семеновна,

д.ф.м.н, профессор кафедры вычислительных методов

Мухин Сергей Иванович

1. Течение вещества в оболочке двойной звездной системы

2. Локальные вихревые атмосферные течения при новороссийской боре (бора - сильный холодный порывистый местный ветер)

3. Сложный режим течения вязкого газа в пространстве между двумя коаксиально вращающимися цилиндрами (разнонаправленное вращение)

4. Сложный режим течения вязкого газа в пространстве между двумя коаксиально вращающимися концентрическими сферами (разнонаправленное вращение)

5. Автоматическое построение реалистичной 3D модели сосудистой системы по данным пространственного графа в комплексе CVSS (Cardio-Vascular Simulation System)

6. Визуализация результатов гемодинамических расчетов в комплексе CVSS (Cardio-Vascular Simulation System)

В ходе работы семинара студенты имеют возможность познакомиться с различными аспектами постановки и решения прикладных задач динамики сплошной среды. В основе математических моделей в подобных задачах лежит приближение «сплошности» вещества, то есть предположение о том, что количество микрочастиц (молекул, атомов, ионов и т.д.) в его достаточно малом объеме чрезвычайно велико, а длина свободного пробега частиц до взаимодействия с другими частицами пренебрежимо мала по сравнению с характерным размером задачи. Это предположение позволяет рассматривать лишь некоторые усредненные характеристики объема, не интересуясь поведением отдельных частиц. В математическом отношении это позволяет использовать для описания характеристик среды хорошо разработанный аппарат функций непрерывного аргумента, дифференциальное и интегральное исчисление. Опираясь на приближения сплошной среды и другие физические закономерности, такие, как, например, законы сохранения, строятся различные математические модели. Примерами могут служить: система уравнений Эйлера, описывающая динамику сжимаемого газа; уравнения Навье-Стокса для вязкой несжимаемой жидкости; уравнения гемодинамики, используемые для описания движения крови по эластичным сосудам. Подобные системы уравнений в частных производных, как правило, являются нелинейными, нестационарными и пространственно многомерными, что определяет зачастую непреодолимые сложности их аналитического исследования. В большинстве случаев нахождение аналитических решений возможно лишь для некоторых частных, упрощенных вариантов исходной задачи. Поэтому, несмотря на то, что в ходе многолетних работ в этой области получено множество интересных результатов, универсальных методов решения таких систем не существует и по сей день. Это в полной мере относится и к численным методам их решения. Связано это с тем, что различные варианты аппроксимации приводят к системам нелинейных алгебраических уравнений, исследование и решение которых также представляет немалую сложность. Кроме этого, соответствующие разностные схемы «близки» к исходным системам дифференциальным уравнений лишь в асимптотическом смысле, то есть при неограниченном измельчении шагов сетки. На практике же в ходе решения прикладных задач необходимо получать физически адекватные разностные решения на достаточно грубых сетка, что обусловлено ограничениями вычислительных ресурсов. Это диктует необходимость изучать и развивать подходы к построению вычислительных методов решения задач сплошной среды. При решении прикладных задач классические математические модели сплошной среды модифицируются с учетом различных дополнительных факторов, влияющих на течение вещества. К таковым можно отнести электромагнитные и гравитационные поля, процессы тепло- и электропроводности, химические реакции, многофазность среды и т.д. Учет подобных явлений во многом определяет специфику конкретной задачи и позволяет выявить эффекты связанные с влиянием того или иного фактора. В качестве примеров остановимся на некоторых задачах в решении которых принимали участие студенты семинара. В качестве первой рассмотрим задачу математического моделирования газодинамических процессов в двойной звездной системе. Для двойных звездных систем, вращающихся вокруг общего центра масс, характерно перетекание газа между компонентами системы и образование газовых дисков, которые называют аккреционными. Процессы в аккреционных дисках оказывают существенное влияние на эволюцию звезд и, если звезда является черной дырой, могут являться единственным источником излучения в ее окрестности, что имеет принципиальное значение для наблюдений. Моделировался процесс эволюции аккреционного диска двойной звездной системы, который описывался системой уравнений газовой динамики Эйлера. Отметим, что несмотря на то, что межзвездная среда представляет собой разреженный газ, характерные для задачи расстояния настолько велики, что приближение сплошной среды здесь вполне оправдано. В системе уравнений дополнительно учитывались силы гравитации обеих компонент и, в силу выбора вращающейся неинерциальной системы координат, центробежная и кориолисова силы. Для решения задачи были проведены двумерные и трехмерные газодинамические расчеты на неравномерных разностных сетках. Показано, что характерной для аккреционных дисков двойной системы является структура, содержащая две спиральные волны, которые являются одним из важных механизмов перераспределения углового момента в веществе диска (см. рис.1).

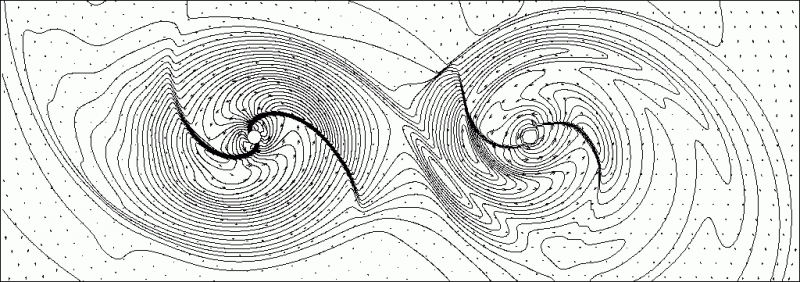
Рис.1. Спиральные структуры аккреционных дисков в двойной звездной системе

В ходе численного решения следующей задачи исследовались процессы возникновения ветров бора в бухте Новороссийска (бора – сильный холодный порывистый местный ветер). Бора наблюдаются на берегах морей, отделенных от континента горными хребтами, в частности, на побережьях Адриатического моря, Хорватии, Новой Земли, Чукотки, в Геленджикской бухте и на берегах Байкала (сарма). В окрестности Новороссийска, который расположен между горным хребтом и морем, условием возникновения боры служит установление области высокого давления над Европейской частью территории России и области низкого давления над Черным морем. Если со стороны суши к горному хребту подходит холодный воздушный фронт, то холодный воздух переваливает через перевал высотой около 430м, который расположен над Новороссийском, и устремляется вниз вдоль крутого склона под действием силы тяжести. В Новороссийске при боре часто наблюдаются порывы ветра в 40м/с, а в отдельных случаях фиксировались значения в 60м/с и даже 80м/с. Температура воздуха при боре может понижаться на 20°C и более. Закономерности возникновения подобных явлений до конца не выяснены.

Предложена математическая модель, основанная на двумерных нестационарных уравнениях газовой динамики с учетом гравитации, описывающая вихревые течения воздушных масс в атмосфере. Моделировалось движение воздушного фронта через прибрежный хребет с последующим возникновением турбулентного течения над морской поверхностью. Выявлялись причины, приводящие к ураганным порывам ветра на поверхности моря, с которыми связаны возможные катастрофические последствия в прибрежной полосе. Полученная в расчетах картина нестационарного вихревого течения, развивающаяся вблизи поверхности моря, адекватна реально наблюдаемым явлениям, сопровождающим бору (см. рис 2).

Рис.2. Вихревое течение при боре

Результаты серии вычислительных экспериментов позволяют выяснить механизм возникновения и развития изучаемого атмосферного явления. Причина его – сдвиговая неустойчивость, возникающая на границе втекающего потока газа и неподвижной в начальной момент атмосферы. Активно развиваясь, эта неустойчивость порождает процесс преобразования кинетической и потенциальной (гравитационной) энергии поступающих воздушных масс в энергию развивающегося у поверхности моря резко нестационарного вихревого течения, именуемого ветром бора.

Как вытекает из приведенных выше примеров основным этапом решения прикладных задач сплошной среды является проведение серии многомерных численных расчетов, в которых с целью детального исследования моделируемых явлений варьируются различные параметры. Здесь принципиальное значение имеет эффективность программного кода и максимальное использование параллельной архитектуры как современных персональных компьютеров, так и суперЭВМ. В ходе работы семинара соответствующие вопросы также активно обсуждаются.

Так, в рамках одной из дипломных работ разрабатывалась параллельная модификация написанного ранее последовательного программного кода, реализующего трехмерные газодинамические расчеты по явной потоковой разностной схеме повышенного порядка точности в сферических координатах. Исследовались способы эффективного распараллеливания применительно к системам с массово-параллельной архитектурой (MPP), представителем которых является успешно функционирующий на факультете суперкомпьютер Blue Gene/P, который и использовался для тестирования разрабатываемых алгоритмов. Целесообразно кратко описать аппаратные особенности этого суперкомпьютера. Каждый вычислительный узел Blue Gene/P состоит из четырех процессорных ядер (3,4 GFlop/sec), собственной оперативной памяти (2 ГБ) и сетевых интерфейсов. Узлы объединяются в карты (32 узла), а карты в стойки (32 карты). На факультете таких стоек две (на момент тестирования), то есть имеется 2048 узлов (8192 процессорных ядер = 27,9 терафлопс). Все вычислительные узлы управляются «легковесными» Linux-подобными операционными системами и объединены в высокоскоростную сеть, имеющую выход на внешние устройства. Подобная архитектура обладает высокой технологичностью и легкостью масштабирования, но вместе с тем и определяет существенные трудности при разработке вычислительных алгоритмов.

Казалось бы на такой системе при реализации параллельных вычислений с использованием всех узлов можно достичь «идеального» ускорения в 2048 раз по сравнению с последовательным расчетом на одном узле. Однако такой показатель в реальных задачах не достижим даже теоретически. Связано это с тем, что на практике приходится находить компромисс между равномерным распределением загрузки (данными и вычислениями) всех задействованных узлов и необходимым для этого обменом данными между узлами, зачастую требующим синхронизации процессов на различных узлах.

В рамках описываемой работы исследованы различные методы декомпозиции области вычислений (распределения данных между узлами), учитывающие специфику используемой разностной схемы. Разработана параллельная модификация вычислительного алгоритма на основе технологии MPI с оптимальным соотношения временных затрат на вычисления и обмен данными между узлами. Проведена серия трехмерных нестационарных расчетов тестовой задачи о распаде сферического разрыва на различных сетках и с различным количеством вычислительных узлов.

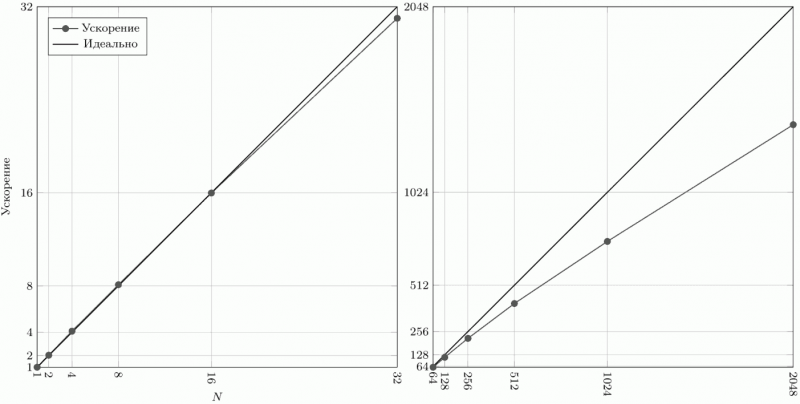
Рис.3. Ускорение при использовании различного количества вычислительных узлов

Естественно, что эффективность распараллеливания зависит не только от способа декомпозиции, но и от размерности разностной сетки, а также количества задействованных вычислительных узлов. На рис.3 продемонстрированы показатели абсолютного ускорения (по времени) для различного количества узлов при расчете на сетке, содержащей 128x256x128 (более 4 миллионов) ячеек. Как легко видеть, с ростом количества узлов этот показатель все больше отклоняется от идеального в сторону уменьшения. Это объясняется увеличением объема пересылок между узлами, в ходе которых вычисления простаивают. Тем не менее, при полном использовании всего вычислительного ресурса Blue Gene/P (2048 узлов) удается достигнуть ускорения в 1397 раз (68% от идеального). Чтобы представить этот результат более наглядно, заметим что указанный расчет, который продолжался 10 часов (более 6 миллиона шагов по времени), с использованием лишь одного узла занял бы более полутора лет.

Еще одной областью, тесно связанной с проведением вычислительных экспериментов, является визуализация результатов многомерных нестационарных расчетов. Руководители и студенты семинара активно работают и в этом направлении. Одним из результатов этой деятельности является разработанный программный комплекс CLCView (Calculated Data Viewer) предназначено для визуализации результатов трехмерных нестационарных расчетов на неравномерных ортогональных сетках в операционных системах семейства Windows. Программа универсальна в том смысле, что позволяет осуществить настройку на файлы данных конкретного расчета, если структура этих файлов удовлетворяет достаточно естественным требованиям. После настройки программа позволяет выбирать из файлов данные, необходимые для ее работы, и строить картину линий уровня совместно картиной векторного поля (см. рис.1, рис.2), а также графики заданных сечений трехмерных сеточных функций. Реализованы все необходимые операции с изображением: масштабирование, скроллинг, увеличение заданных фрагментов, вывод видимого фрагмента изображения на устройства печати (с полным использованием их разрешающей способности) или сохранение в графические файлы различных форматов. Наряду с линиями уровня осуществляется построение цветовой «заливки» в произвольной палитре, задаваемой пользователем.

Предусмотрена возможность так называемой пакетной обработки результатов расчета. Задается набор файлов данных результатов, соответствующий последовательным моментам времени. После этого без дальнейшего вмешательства пользователя либо строится последовательность изображений заданных сечений сеточных функций, сохраняемая в графические файлы, либо генерируется видео в одном из форматов стандарта MPEG4. Программа позволяет генерировать полноформатное (в том числе и Full HD) видео, иллюстрирующее результаты расчетов.

Основной целью разработки программы ClcView являлось создание простого и эффективного средства визуального анализа результатов нестационарных расчетов. Программа изначально была ориентирована на вычислительные задачи, которые приходилось решать руководителям семинара, а это в основном двумерные и трехмерные газодинамические расчеты на ортогональных (равномерных и неравномерных) сетках. Существующие «большие» программные пакеты, конечно, также подходят для визуализации результатов таких расчетов, однако требуют дополнительных усилий для подготовки данных для своей работы. Кроме того, «универсальность» таких пакетов зачастую приводит к снижению производительности при решении достаточно простых задач визуализации. При разработке ClcView основной акцент делался на отсутствии дублирования данных (одни и те же данные для возобновления расчета и визуализации), простоте настройки программы на данные конкретного расчета и максимальной производительности визуализации его результатов. Поскольку для нестационарных расчетов особенно важной является возможность анализа динамики изменения сеточных функций во времени, особое внимание уделялось производительности генерации видео на основе цветовой «заливки». В результате удалось достигнуть производительности близкой к показателям «реального времени» (25 кадров в секунду) при генерации полноформатного видео в формате MPEG4 по данным нестационарных расчетов на достаточно подробных сетках.

Рис.4. Трехмерный граф сердечнососудистой системы человека

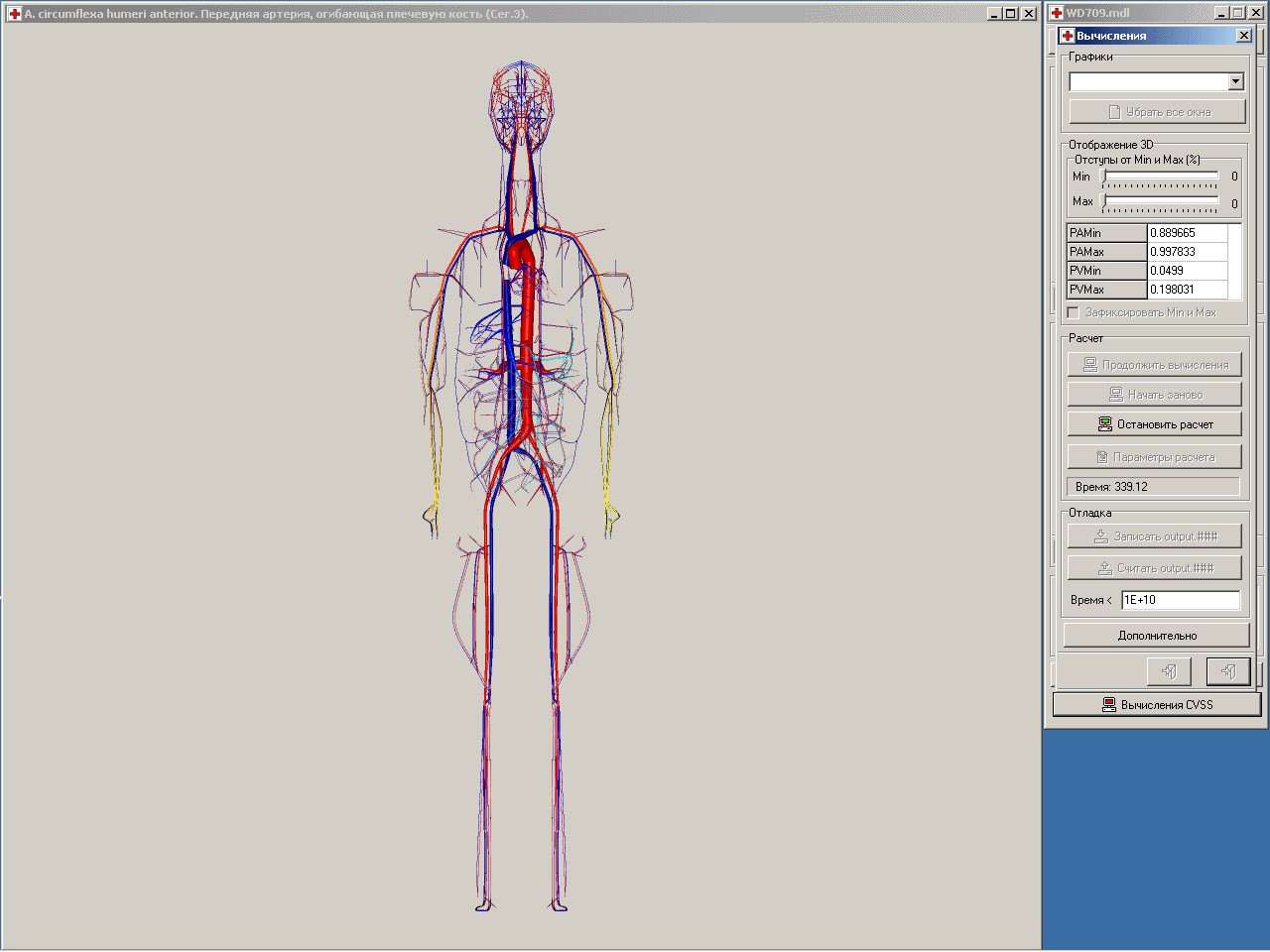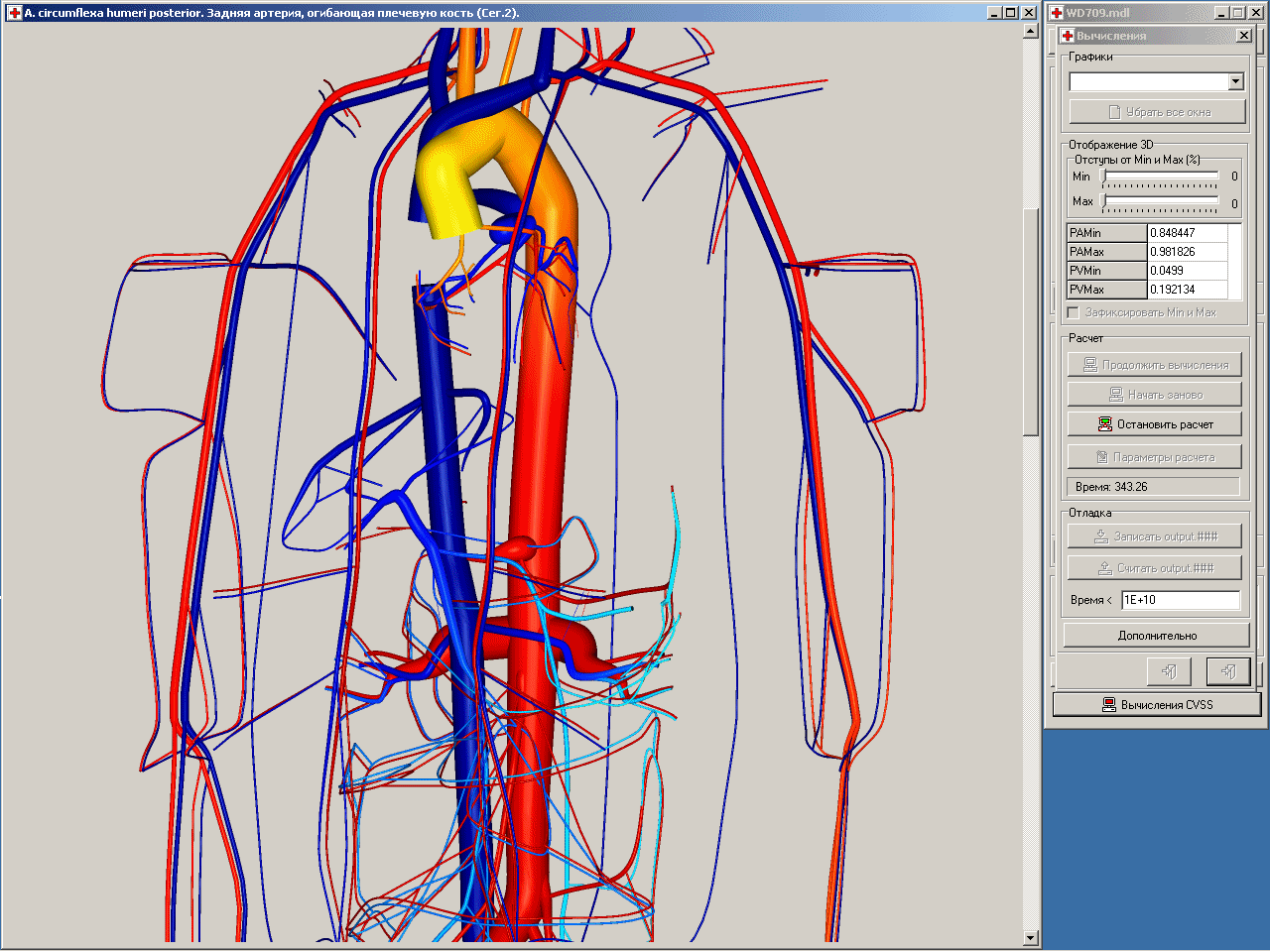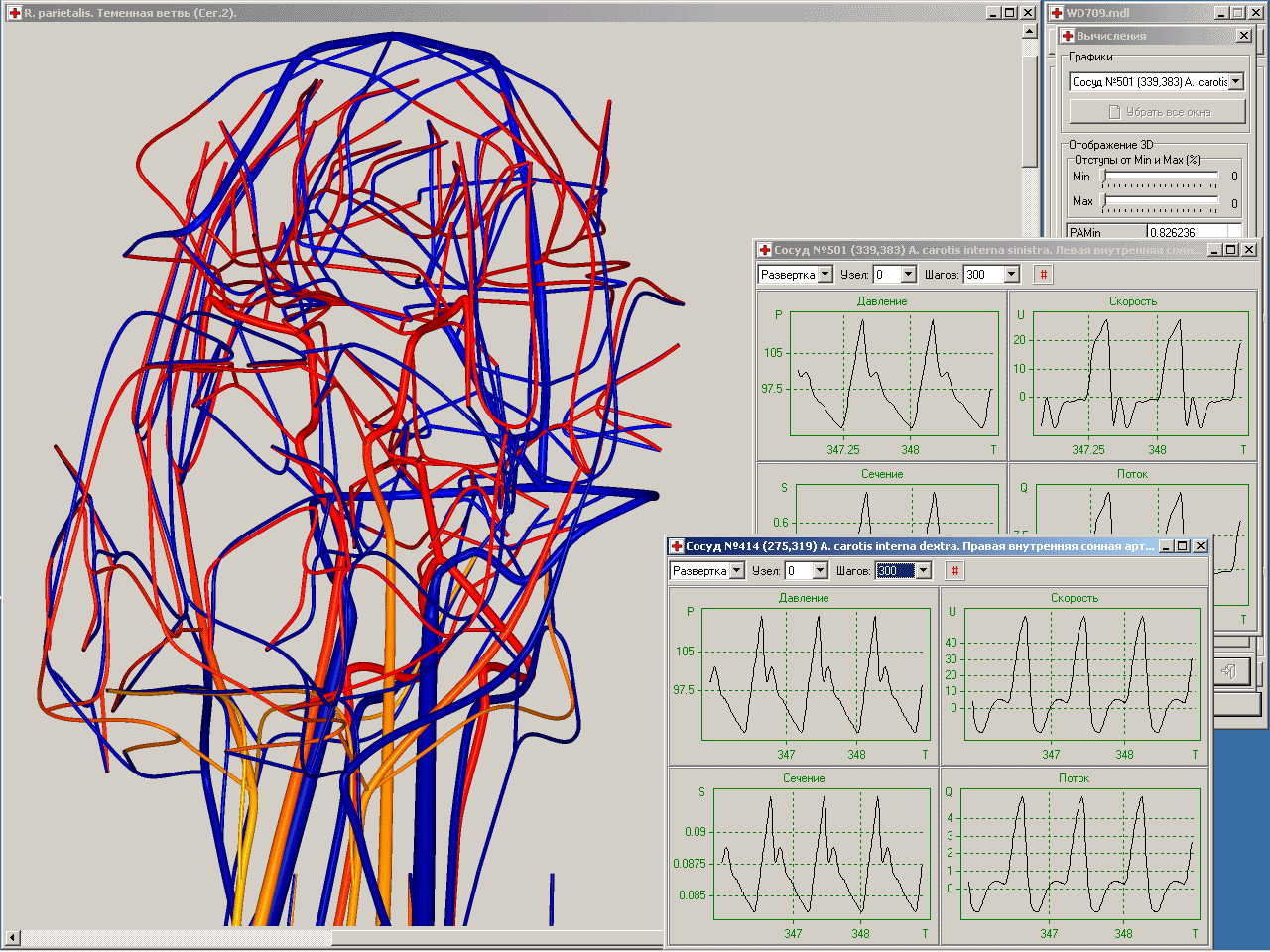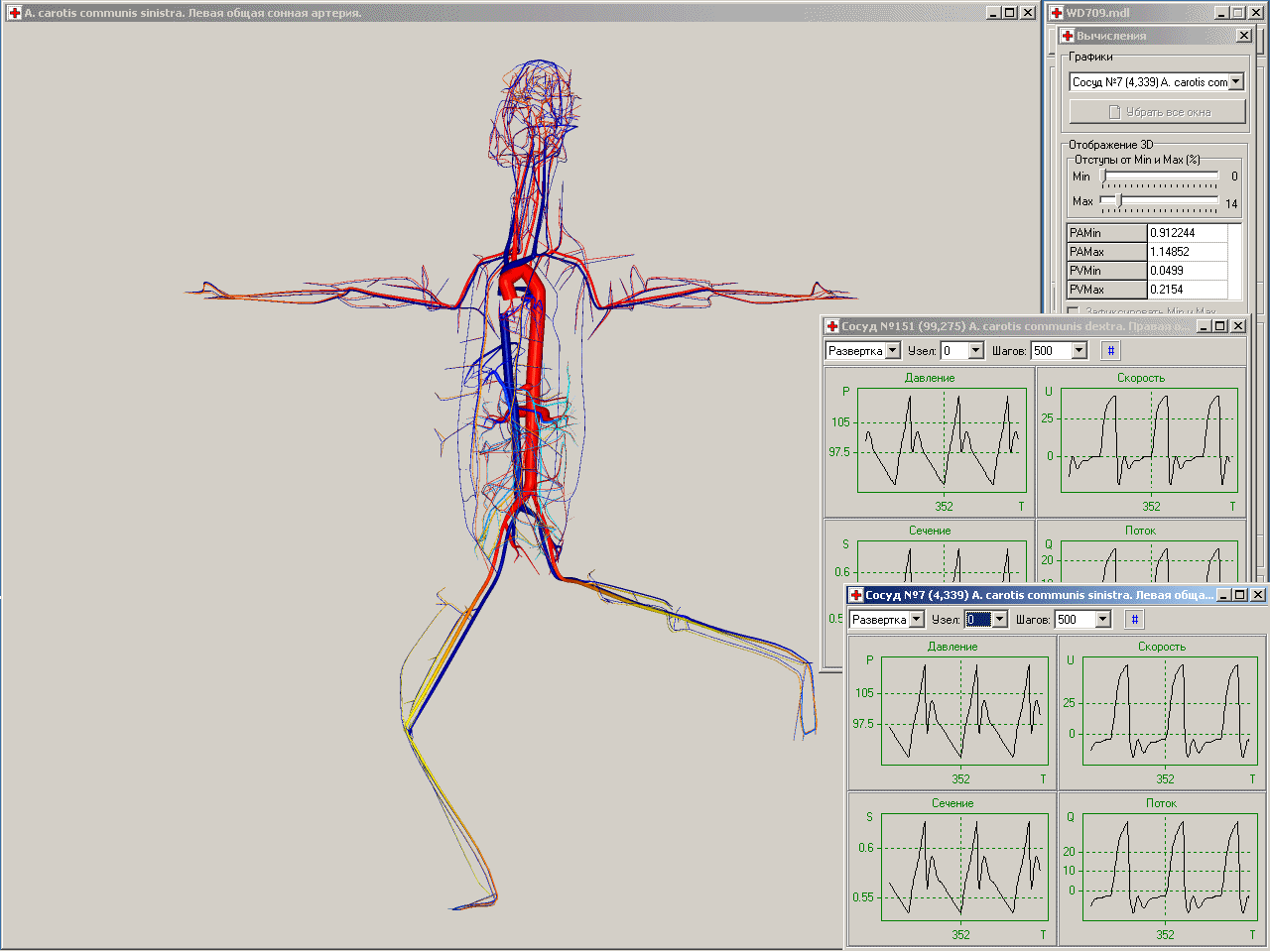
Еще одним примером тесной взаимосвязи математического моделирования и решения задач визуализации может служить разработанный руководителями семинара управляющий модуль расчетного комплекса CVSS (Cardio-Vascular Simulation System). Этот комплекс разрабатывался на кафедре вычислительных методов в течении многих лет для моделирования течения крови в сердечнососудистой системе человека. Управляющий модуль позволяет в интерактивном режиме создавать трехмерные модели (графы) системы сосудов (см. рис.4), задавать данные на узлах и ребрах графа, необходимые для последующей работы солвера (вычислительного модуля). Допускается независимая работа нескольких пользователей с данными модели с последующей интеграцией внесенных ими изменений и дополнений. Реализованы групповые операции задания данных на сходных по своим свойствам сосудах и узлах их ветвления. В качестве базовой рассматривается каркасная пространственная модель трехмерного графа, требующая минимального объема вводимой информации. Разработанные и реализованные в комплексе алгоритмы позволяют по данным каркасной модели автоматически строить реалистичную объемную трехмерную модель графа сосудистой системы (см. рис.5), используемую в дальнейшем как для визуального контроля корректности данных, так и для визуализации результатов расчета.

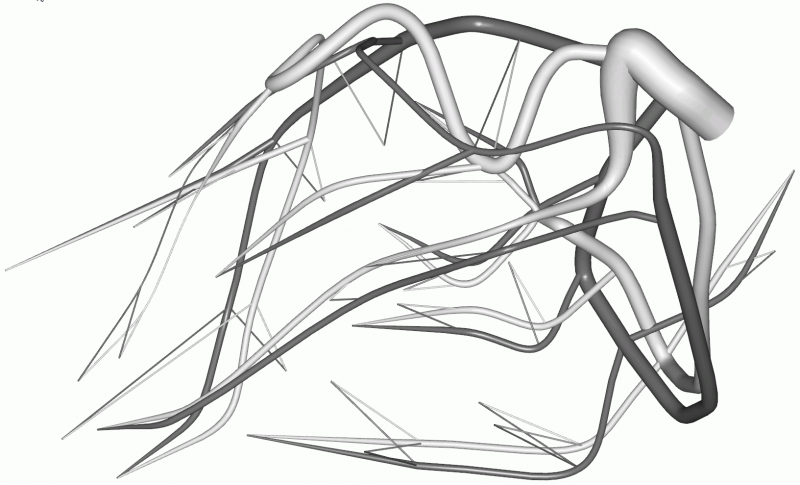
Рис.5. Фрагмент сосудистой системы

Управляющий модуль использует современные аппаратные возможности многопотоковых вычислений. В ходе работы солвера процесс вычислений запускается в виде отдельного, независимого от работы управляющего модуля, потока. Параллельно с процессом вычислений управляющий модуль осуществляет интерактивную обработку текущих результатов. Имеется, в частности, возможность менять ракурс и масштаб изображения объемной модели, на которой цветом выводится текущее давление на всех сосудах артериальной и венозной части графа, одновременно отображать временные развертки параметров на любом количестве сосудов, управлять выводом графической информации, прерывать и возобновлять расчет после изменения параметров солвера. Система хранения данных модели предусматривает их последующее объединение с данными расчета. Это позволяет продолжить моделирование течения на графе сосудов с момента времени последнего прерывания расчета даже в случае изменения топологии графа (пережатие сосуда, добавление шунта и т.п.)

Подытоживая этот далеко не полный обзор научной деятельности семинара, представляется целесообразном очертить круг основных направлений, в которых студенты могут реализовать свои интересы:

– разработка математических моделей сплошной среды;

– исследование моделей путем аналитического и численного решения упрощенных (модельных) задач;

– изучение и развитие вычислительных методов решения возникающих систем уравнений;

– исследование и применение к решению прикладных задач существующих вычислительных методов;

– разработка и реализация ориентированных на суперЭВМ параллельных алгоритмов расчета прикладных задач динамики сплошной среды;

– разработка и реализация методов решения задач визуализации результатов расчетов.

Смотреть видео